植物の美しさや論理性を作る数字｜フィボナッチ数列

「1, 1, 2, 3, 5, 8, 13, 21…」この数列をご存知でしょうか？

イタリアの数学者フィボナッチによって証明された不思議な数字「フィボナッチ数列」です。

地球上に存在する様々な植物や昆虫がこの数列に当てはまった形状をしています。

フィボナッチ数列とは「2つ前の項と1つ前の項を足し合わせていくことでできる数列」のことをさします。

数列は「1,1」から始まり、1, 1, 2, 3, 5, 8, 13, 21, 34, 55…と続いていきます。

黄金比（人が美しいと感じる比率）の式は” 1 : 1.618。フィボナッチ数列を比率で表していくと

2 : 3 ＝ 1 : 1.5、3 : 5 ≒ 1 : 1.666666、5 : 8 ＝ 1 : 1.6、8 : 13 ＝ 1 : 1.625、13 : 21 ＝ 1 : 1.61538

フィボナッチ数列は数が増えるにつれ、その比率はどんどん黄金比に近づいていきます。

様々な植物や昆虫がこの数列に当てはまっていくのは必然な気がしますね。

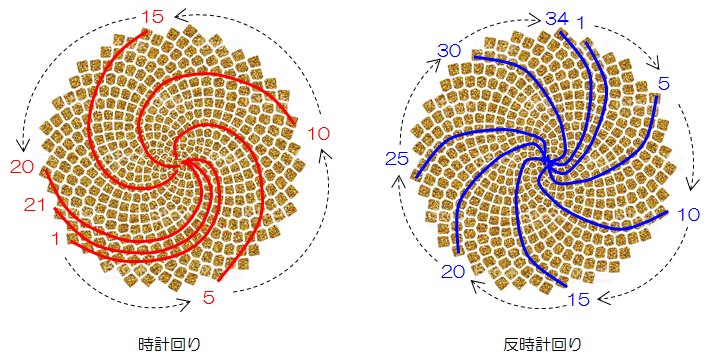
赤い線は螺旋状の種の並びを示しています。線はひまわりの中心から外側に向かって時計回りになっています。

また、見方を変えると、青い線のように反時計回りに種が配置されているようにも見えます。

このように、時計回りと反時計回りの種の配置を持つひまわりですが、時計回りと反時計回りの線の数は

• 時計回りが21本、反時計回りが34本
• 時計回りが34本、反時計回りが55本
• 時計回りが55本、反時計回りが89本

となるのです。この数字は全てフィボナッチ数列の数字と同一です。

引用サイト：https://analytics-notty.tech/fibonacci-and-goldenratio-in-sunflower/

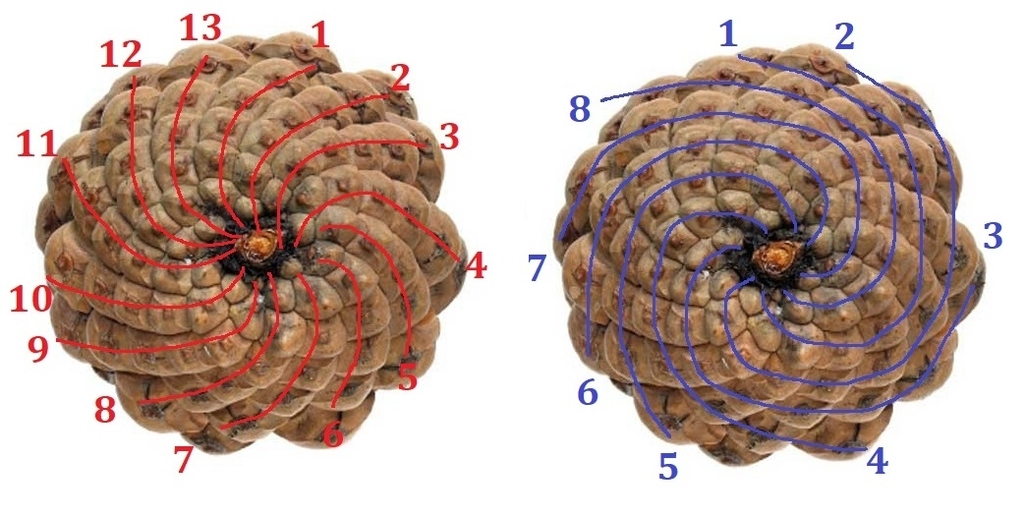
松ぼっくりを根本から見たとき、松かさの並びの渦の本数を数えると、時計回りで13本、反時計回りで8本になりました。8も13もフィボナッチ数です。

引用サイト：http://hibiyastudy.hatenablog.com/entry/math/fibonacci/

パイナップル（スナックパイン）も 13本、8本、5本のらせんを順に示している。

引用サイト：http://u0u1.net/Y3Rr

放射状に10本、かと思いきや、こちらも5本の螺旋が存在しています。

引用サイト：http://u0u1.net/Y3Rr

上記以外にも、多くの植物や果物にフィボナッチ数列が存在しています。

いかがでしたでしょうか？

植物もおかれた環境や目的に見合う明確な形や数字が存在します。

家造りも同じです。人間が本能で心地良いと感じる空間作り、お客様のライフスタイルや目的にあった間取り、その土地に合った設計が必要だと考えています。

そのため私たちは、人間工学や建築医学、いつの時代でも変わることのない普遍的なデザインを追求し続けています。